Common sense and chemical intuition suggest that the higher the temperature, the faster a given chemical reaction will proceed. Quantitatively this relationship between the rate a reaction proceeds and its temperature is determined by the Arrhenius Equation. At higher temperatures, the probability that two molecules will collide is higher. This higher collision rate results in a higher kinetic energy, which has an effect on the activation energy of the reaction. The activation energy is the amount of energy required to ensure that a reaction happens.

This calculator calculates the effect of temperature on reaction rates using the Arrhenius equation.

k=A*exp^(-E_a/R*T)

where k is the rate coefficient, A is a constant, E_a is the activation energy, R is the universal gas constant, and T is the temperature (in kelvin).

R has the value of 8.314 x 10^-3 kJ mol^-1K^-1

You should use this calculator to investigate the influence of temperature on the rate coefficient.

This calculator allows you to perform three different calculations:

Calculate A given k, E_a, and T
Calculate k given A, E_a, and T
Calculate E_a given A, k, and T

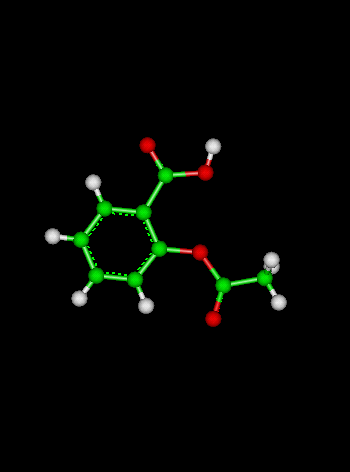
Sample Problem:

The reaction:

2NO₂(g) -----> 2NO(g) + O₂(g)

has a rate coefficient of 1.0 x 10^-10 s^-1 at 300 K and an activation energy of 111 kJ mol^-1. What is the rate coefficient at 273 K?

(Solution: calculate the value of A for a temperature of 300 K, then use the calculated value of A to calculate k at a temperature of 273 K. We generally assume that A and the activation energy E_ado not vary with temperature).

Calculate k given A, E_a, and T:

Calculate E_a given A, k, and T:

Back to the kinetics page.

Developed by

Shodor
in cooperation with the Department of Chemistry,
The University of North Carolina at Chapel Hill

The Arrhenius Equation

Background reading:

Sample Problem:

Calculate A given k, E_a, and T:

Input Value(s):

Result(s):

Calculate k given A, E_a, and T:

Input Value(s):

Result(s):

Calculate E_a given A, k, and T:

Input Value(s):

Result(s):

The Arrhenius Equation

Background reading:

Sample Problem:

Calculate A given k, Ea, and T:

Input Value(s):

Result(s):

Calculate k given A, Ea, and T:

Input Value(s):

Result(s):

Calculate Ea given A, k, and T:

Input Value(s):

Result(s):

Calculate A given k, E_a, and T:

Calculate k given A, E_a, and T:

Calculate E_a given A, k, and T: