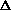p because pressure decreases with height. By moving a few terms around, we see that the change in pressure with height is equal to air density times gravity.
Now, since we know how to relate temperature and density (via the Equation of State), we can determine how rapidly pressure will decrease at a given temperature. Of course you must assume a hydrostatic atmosphere to see this relationship. This becomes very important when we talk about stability in Session 6.
There are some important things to know about a hydrostatic situation. First, it is a very good approximation of the real atmosphere on large scales away from frontal zones. However, in any region where there is significant vertical acceleration (frontal zones), the hydrostatic equation will not hold true, as the forces listed above are not balanced. This also holds true for smaller scales, such as urban areas or local storms. Because there is so much turbulence in metropolitan areas, one cannot assume a hydrostatic situation without being significantly off from reality. It is similar for small areas with local storms. Clearly, under a thunderstorm there is upward air motion, and the hydrostatic equation is therefore inaccurate.
The Shodor
Education Foundation, Inc.