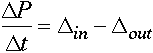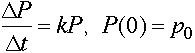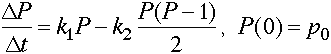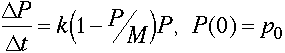Dr. Holly Hirst Modeling PopulationsPopulation growth is one of the easiest phenomona to use to learn about modeling because simple models can be built very intuitively. Here are the models I use with my modeling classes to teach about the modeling process. I have implemented them all in Stella below.
Suppose we want to model a how a population changes over time. Let P be the biomass at any given time and t be the time since starting to observe the system. The change in population over time is equal to increases during that time minus decreases during that time.
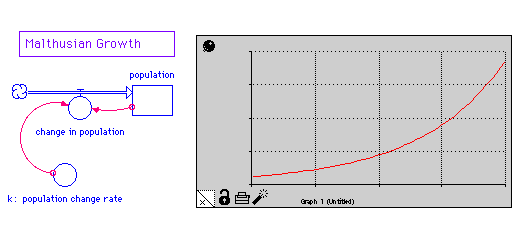
How might we model these changes? The more the merrier (Malthusian Growth): The simplest idea would be to assume that the increase rate was proportional to the amount present. (The more rabbits the more rabbit babies they make). The same goes for the death term. (The more rabbits the more they compete for food causing deaths). This gives:
So:
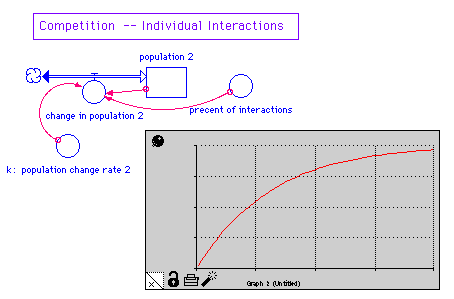
Click on the picture for a clearer, larger version. We get exponential growth (always increasing) from this. So this simple idea for death isn't going to adequately reflect competition. Competition I: How can we introduce competition? Let the deaths be proportional to average number of 2-individual interactions:
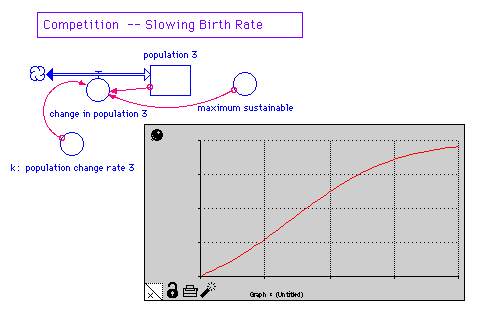
Click on the picture for a clearer, larger version. Here we get a leveling off. Do rabbits really fight? Is there another way to model competition? Competition II: Let the growth rate decreases to zero as maximum sustainable population (M) is approached:
Click on the picture for a clearer, larger version. This other way of thinking gives similar behavior. This behavior is called logistic growth. What happens when we add another species as a predator? Look at Predator-Prey Models Last update on: June 1, 1998 Please direct questions and comments about this page to [email protected] © Copyright 1998 The Shodor Education Foundation, Inc. |