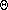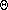))Let's suppose you are working outside on a hot summer day. When you go inside to cool off and check out the score of the big game you are missing, a weather alert comes on calling for severe thunderstorms with large damaging hail. How could such large balls of ice fall from up there when it is so hot down here? And if it is cold enough up there to form ice, why can't we just bring some of that cold air down to cool things off a bit?
The equation of state can help us answer these questions. The equation of state helps us figure out the state of the atmosphere under various conditions. For instance, suppose the air at the surface of the earth is dry and in equilibrium, stable, and has a pressure of 1000 mb (100 kPa), a specific volume of 0.83 m3/kg (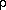
=1.21 kg/m3), and a temperature of 25 C. If we were to lift a volume of that air (without adding any heat to the air) to a height where the pressure was 700 mb (70 kPa), the volume of the parcel would increase and the temperature would decrease in order for the lifted air to assume a pressure of 700 mb like the surrounding air. To say it another way, the parcel would expand to a pressure of 700 mb. Because the parcel was lifted without adding heat, the change of state of the parcel is called a dry adiabatic change. Adiabatic simply means to alter the state of a gas without adding or withdrawing heat from the gas. The change in the temperature with the change in pressure is called the dry adiabatic lapse rate. Through several computations using the laws of thermodynamics, the specific volume cancels and a new equation is used to describe the relationship between the temperature and pressure of the atmosphere during adiabatic expansion and compression. This equation is referred to as Poisson's equation and is written as
To answer our initial questions about hail on a hot day and cold air aloft, the air above is so much colder than the air at the surface because the temperature is in equilibrium with the density and pressure at the height it is residing. So, hail can form on a very hot day because the temperature aloft can be below freezing when the temperature at the surface is quite scorching. But if we were to try to bring that same cold air to the surface, the temperature would increase in order to compensate for the adiabatic compression.
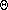For convenience of comparison, meteorologists have defined the potential temperature() as the temperature an air parcel would have if it were expanded or compressed adiabatically to a pressure of 1000 mb (100 kPa). Thus, for the air parcel we lifted, because we started at 1000 mb (100 kPa) with a temperature of 25 C, the potential temperature (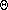) is 25 C. To calculate the potential temperature, Poisson's equation can be rewritten as
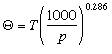
Potential temperature is going to be an important term later when we discuss the vertical stability of the atmosphere. Comparing the potential temperature of a parcel to that of its surroundings can tell us weather a region of air is stable or subject to lifting or sinking. We will see that the issue of stability is a major factor when trying to determine the transport and dispersion of air pollutants. Pollutants trapped in a stable layer can sit stagnant in very high concentrations. Once air becomes unstable and buoyant the air may rise and mix and dilute the pollutants.
Calculating
| You can better familiarize yourself with the concept of potential temperature by computing the potential temperatures of air parcels of different pressures and temperatures using a "pop-up" Javascript calculator. This calculator will compute an unknown variable in the equation above given known values for the remaining two variables. Because this calculator is written in Javascript and uses frames, it requires Netscape 2.02 (or a more recent version). |
The Shodor
Education Foundation, Inc.