Part 3:
Values We Infer
While temperature, humidity, pressure, and wind data tell us much about
current atmospheric conditions, in and of themselves, they tell us little
about future conditions. We can use them, however, to determine the
values of other parameters which are necessary for forecasting and
modeling the atmosphere. Computers now calculate these values for us so
you will not be expected to make these computations yourself during this
course. However, a look at how a few of these parameters are defined
either mathematically or graphically can increase your understanding of
the behavioral influences of the atmosphere.
Equation of State
 If we want to model the behavior of the atmosphere, which is mostly made
up of gases, we must study the natural behavior of gases. All gases are
found to approximate the equation of state. The equation of state
does just what its name suggests. It tells us of the state of a particular
gas under a broad range of conditions. The equation of state defines the
relationship between the temperature (T), density (
If we want to model the behavior of the atmosphere, which is mostly made
up of gases, we must study the natural behavior of gases. All gases are
found to approximate the equation of state. The equation of state
does just what its name suggests. It tells us of the state of a particular
gas under a broad range of conditions. The equation of state defines the
relationship between the temperature (T), density (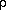 ), and pressure (P) of the gas. These we call
the state variables. The equation of state can be written as
), and pressure (P) of the gas. These we call
the state variables. The equation of state can be written as
P = 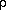 R T
R T
Pressure = Density x Gas Constant x Temperature
where P is measured in pascals (Pa), 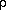 is in grams per cubic meter (kg/m3), T is in degrees Kelvin
(K), and R is in Joules per kilogram
per degree Kelvin (J kg -1 K -1). R is a
proportionality constant and is different for each gas or mixture of
gases. The inverse of density is called specific volume (
is in grams per cubic meter (kg/m3), T is in degrees Kelvin
(K), and R is in Joules per kilogram
per degree Kelvin (J kg -1 K -1). R is a
proportionality constant and is different for each gas or mixture of
gases. The inverse of density is called specific volume ( ) and is defined as the amount of volume
required for one unit of mass at a given temperature and pressure.
Specific volume is commonly expressed as cubic meters of gas per kilogram
of gas (m3/kg). By substituting specific volume for density we
can rewrite the equation of state as
) and is defined as the amount of volume
required for one unit of mass at a given temperature and pressure.
Specific volume is commonly expressed as cubic meters of gas per kilogram
of gas (m3/kg). By substituting specific volume for density we
can rewrite the equation of state as
P  = R T
= R T
Pressure x Specific Volume = Gas Constant x Temperature
Though the atmosphere is a mixture of gases, atmospheric scientists have
discovered that the atmosphere also closely approximates the equation of
state. For the dry atmosphere (i.e., no water vapor present) R = 287
Jkg-1K-1. This means that we can take a sample of
dry air and measure the initial temperature, pressure, and volume. If we
then control one variable and alter another, we can compute the third.
The equation of state is a fundamental law governing the behavior of the
atmosphere under changing conditions. It allows us to predict
temperature, pressure, and density changes in the atmosphere which
ultimately determine stability and motion. These, in turn, drive weather systems and transport pollutants.
Computing
with the
Equation of State
| This link will provide you with a "pop-up" Javascript calculator that will calculate an unknown variable of the equation of state, given values for the other three variables. Because this calculator is written in Javascript and uses frames, it requires Netscape 2.02 (or a more recent version).
|



Developed by
 The Shodor
Education Foundation, Inc.
The Shodor
Education Foundation, Inc.
Copyright © 1996
 If we want to model the behavior of the atmosphere, which is mostly made
up of gases, we must study the natural behavior of gases. All gases are
found to approximate the equation of state. The equation of state
does just what its name suggests. It tells us of the state of a particular
gas under a broad range of conditions. The equation of state defines the
relationship between the temperature (T), density (
If we want to model the behavior of the atmosphere, which is mostly made
up of gases, we must study the natural behavior of gases. All gases are
found to approximate the equation of state. The equation of state
does just what its name suggests. It tells us of the state of a particular
gas under a broad range of conditions. The equation of state defines the
relationship between the temperature (T), density (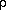 ), and pressure (P) of the gas. These we call
the state variables. The equation of state can be written as
), and pressure (P) of the gas. These we call
the state variables. The equation of state can be written as ) and is defined as the amount of volume
required for one unit of mass at a given temperature and pressure.
Specific volume is commonly expressed as cubic meters of gas per kilogram
of gas (m3/kg). By substituting specific volume for density we
can rewrite the equation of state as
) and is defined as the amount of volume
required for one unit of mass at a given temperature and pressure.
Specific volume is commonly expressed as cubic meters of gas per kilogram
of gas (m3/kg). By substituting specific volume for density we
can rewrite the equation of state as The Shodor
Education Foundation, Inc.
The Shodor
Education Foundation, Inc.