SimSurface Summary

Overview

SimSurface might best be described as a "what-if tool." It is not designed to lead a student through an artificial, preprogrammed "experiment"; rather, it allows the student to have an authentic scientific experience. The process of observation, conjecture, and testing of conjectures (by experimentation and, of course, more observation) is what real scientists do every day. Our hope is that students will find enough interesting questions to ask about the events they observe when using SimSurface to reawaken the innate curiosity that we have as children and which is the real driving force behind most scientific inquiry. SimSurface is a program designed for use in instruction of computational science in general and of the specific numerical techniques used in the program.

SimSurface demonstrates two commonly used computational techniques. The first, simulated annealing, is an often-used method for finding global maxima and minima of complicated multi-dimensional functions. It can be used any time you have a function that gets big when things are bad and small when things are good (or vice-versa). The problem being solved in SimSurface is a minimization of potential energy. The question we are trying to answer is: given n stationary electrons/protons confined to a 2-dimensional surface by four charged walls, what arrangement of electrons has the minimum total energy and is therefore the configuration preferred by nature?

If the user chooses to experiment with the "Application" part of Simsurface, he enters numbers that specify the initial conditions of the surface and electrons (number of electrons and the charge values on the walls).

If instead he chooses to experiment with the "Algorithm" section of Simsurface, he is prompted for values which determine how fast the system cools. The "Architecture" section of SimSurface is not yet functional: the code can only be run on one machine, in this case an SGI Power Challenge.

Typical initial configuration

Typical final configuration

Once the system has reached a minimum energy (to within a specified tolerance), we would like to know what the electrical potential looks like around the electrons. This could of course just be calculated directly at each point, but a much faster and widely used technique called relaxation is actually used to solve Laplace's equation. Laplace's equation says that the net curvature of the potential surface is zero everywhere (del^2 phi=0) on the surface (except at the point charges themselves), but the relaxation method is very easy to understand, even for those that do not fully understand the equation it is solving. It is an iterative process, which at each iteration sets the value of a grid point equal to the average of its 4 neighbors. The charges and walls are held constant throughout this process. SimSurface displays the end result of this process: the potential on the plate.

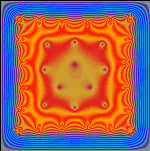
Note that the colored bands in the image are equipotential lines of the field.